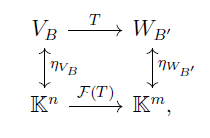
Examples of categories are ubiquitous. For instance, we have the category $\text{FVect}$ whose objects are finite-dimensional vector spaces and morphisms are linear maps, we have the category $\text{Top}$ whose objects are topological spaces and morphisms are continuous maps, we have the category $\text{ProdK}$ whose objects are finite cartesian products of a field $\mathbb{K}$ (with its canonical vector-space structure) and whose morphisms are the functions which are multiplication by matrices, etc. We note that morphisms need not be functions, and objects need not be sets. However, we will not need to discuss that for what follows. A functor between two categories $\mathcal{C}_1$ and $\mathcal{C}_2$ is an association between two categories in the following sense: it takes an object of $\mathcal{C}_1$ to an object of $\mathcal{C}_2$, and a morphism between two objects in $\mathcal{C}_1$ to a morphism between the two objects associated in $\mathcal{C}_2$. We also require that composition of morphisms is taken to composition of morphisms, and that the identity is taken to the identity. An example will come shortly.
Consider now the category $\text{BFVert}$, where the objects are finite-dimensional vector spaces $V$, considered together with an ordered basis $B$ (that is, the objects are $(V,B)$) and the morphisms are the linear transformations. The "identification"{} between linear transformations and matrices can now be stated as follows:
Proposition: There exists a functor $\mathcal{F}: \text{BFVert} \rightarrow \text{ProdK}$ which sends the objects $V_B$ of $\text{BFVert}$ to the space $\mathbb{K}^n$, where $n=\dim(V)$, and makes the following diagram commute:
where $\mathbb{K}^n=\mathcal{F}(V_B)$, $\mathbb{K}^m=\mathcal{F}(W_{B'})$ and $\eta_{V_B}$, $\eta_{W_B'}$ are the isomorphisms (in the vector-space sense) which take the elements of the basis and send them, orderly, to the canonical basis of $\mathbb{K}^n$ and $\mathbb{K}^m$, respectively.
Proof: The proof of this is what is done in Linear Algebra, so we leave it as exercise. $\blacksquare$
Note that the matrix associated to $T$ is, therefore, $\mathcal{F}(T)$. Note also that a functor satisfying such properties is unique, as easily verified by the fact that the coefficients of the matrix is imposed by the properties of the functor.
Having stated the identification between matrices and linear maps in such a clear and precise way, it eludes me how Category Theory took so long to be developed, waiting up to Algebraic Topology to force it to surface.
We end this discussion by noting that the $\eta$ isomorphisms which appear in the diagram also have a nice generalization. They constitute a natural transformation between the identity functor and the functor $\mathcal{F}$. Interested readers are invited to look up the concept.
 RSS Feed
RSS Feed
