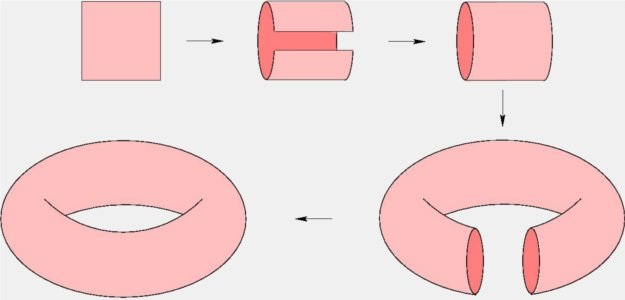
When you take a square, and identify a point of each side with its "opposite", you get a torus.
With that in mind, let's begin:
Definition: If $X$ is a topological space and we have a partition of $X$, call $X^*$ the set of those subsets that form the partition. Give $X^*$ the following topology: A subset of $X^*$ (which is a collection of subsets of X) is open if and only if the union of that collection is open in $X$. This is the quotient space.
Equivalently, if $X$ is a topological space and we have an equivalence relation $\sim$, call $X/ \sim$ the quotient space (meaning, the set of equivalence classes). We then have the map: $\pi :X \rightarrow X / \sim$ that takes $x$ to its equivalence class $\bar{x}$. Now, give $X/ \sim$ the following topology: $U'$ is open in $X/ \sim$ if and only if $\pi^{-1}(U')$ is open in $X$. This is the quotient space.
It may not be easy to see that they are equivalent at a first glance if you are not familiar with equivalence relations, or with topology, but a bit of thought will make it clear. I will adopt the latter definition in the calculations (but will write $X/ \sim $ as $X^*$ for convenience) since it is more algebraic, hence, easier to handle.
Now, before introducing the next useful theorem, let me give some acquaintance to commutative diagrams. Consider the isomorphism theorem:
Isomorphism Theorem: Given an homomorphism $f: G \rightarrow H$ between two groups, we have $\displaystyle G/\ker(f) \simeq Im(\phi)$.
What this theorem says can be given more precision, in the following language:
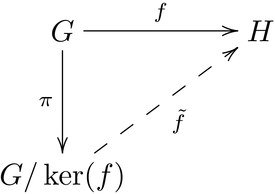
Isomorphism Theorem: Every homomorphism $f: G \rightarrow H$ between two groups induces an injective homomorphism $\bar{f}: G / \ker(\phi) \rightarrow H$ making the following diagram commute (meaning: $f= \bar{f} o \pi$)
Take a minute to understand this and then we can proceed:
Proposition: Given $X, Y$ topological spaces, a continuous $f:X\rightarrow Y$ which is constant on every equivalence class induces a continuous map $f^*: X^* \rightarrow Y$ making the following diagram commute:
Define $f^*(\bar{x})=f(x)$. It is well-defined by the previous observation, and obviously $f=f^*o\pi$. It remains to show that $f^*$ is continuous. Lets show pre-image of open is open! But, a set $U$ is open in $X^*$ if and only if $\pi^{-1} U$ is open in $X$. So, we have to show that, for every open $V$ in $Y$, $\pi^{-1} o f^{*-1} (V)$ is open. But this set is exactly $f^{-1}(V)$. Since $f$ is continuous, we have proved $f^*$ is continuous.
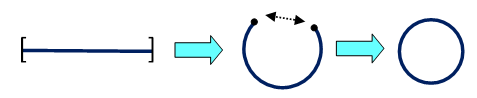
Let's see an application of this and prove... that the circle is a segment where you identify the endpoints!
Consider $I:=[0,2\pi]$, and $S^1:=(\cos(t),\sin(t))$, for $t \in [0,2\pi)$. Now, make the following equivalence relation in $I$: every point is equivalent only to itself, except $0$ and $2\pi$, which are equivalent (they are in the same equivalence class). Therefore, we have $I^*$
Take the map $f: I \rightarrow S^1$ that takes $x$ to $(\cos(x), \sin(x))$. Note that $f(0)=f(1)$. So, $f$ satisfies the hypothesis of our preceding proposition (namely, it is constant in every class!). Then, we have an induced continuous map $f^*: I^* \rightarrow S^1$. (Note that $f^*$ is bijective). Now, take the following map: $g: S^1 \rightarrow I^* $ that takes $(\cos(x), \sin(x))$ to $\bar{x}$). It is obviously continuous on all points, except possibly at $f(1,0)$ (since all other classes are points). But the neighbourhoods of $f^*(1,0)=\bar{1}=\bar{0}$, now that we are at the quotient space, must "contain" a neighbourhood of $1$ and a neighbourhood of $0$. Why? Suppose you have a neighbourhood $\bar{U}$ of $\bar{1}$. So, $\pi^{-1}(\bar{U})$ must be an open set containing $0$ and $1$. Therefore, there are two small intervals around $0$ and $1$ in $\pi^{-1}(\bar{U})$, which will be taken to the corresponding classes. So, this $g$ is continuous, since we can take a small enough piece of the circle around $(1,0)$ for which the function will fall inside those intervals. But this $g$ is the inverse of $f^*$. So, we found a homeomorphism. We could also do something more elegant (but would need more knowledge about topology): Since $I$ is compact, so is $I^*$. But $f^*$ is bijective, and $S^1$ hausdorff, so $f^*$ is in fact a homeomorphism.
In Pt.3, we shall talk about another style of glueing things.
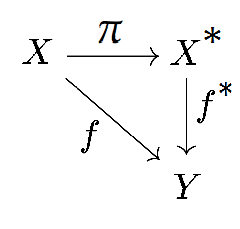
 RSS Feed
RSS Feed
